Trên lớp, học sinh đã được giảng dạy lý thuyết để có thể hình dung hướng giải cho những dạng toán về cách tính các giá trị biểu thức lớp 9. Nhưng tên thực tế, dạng toán này có những cách biến hóa rất đa dạng và đôi khi học sinh sẽ cảm thấy lạ và lúng túng trong việc tìm cách giải. Hiểu được điều đó, sau đây sẽ là tổng kết lý thuyết và đi vào cách giải cụ thể từng bài.
Table of Contents
Nắm vững lý thuyết để vững vàng làm bài
Nắm vững lý thuyết trước khi tính toán giá trị biểu thức là một phần quan trọng của việc học về cách tính giá trị biểu thức lớp 9. Lý thuyết giúp học sinh hiểu rõ ý nghĩa của các toán tử và ký hiệu trong biểu thức. Nếu các em không hiểu các khái niệm cơ bản như tử số, mẫu số, biến, hằng số, dấu ngoặc thì rất có thể sẽ gặp nhiều khó khăn trong việc hiểu và làm cách tính giá trị biểu thức lớp 9.
Lý thuyết giúp học sinh hiểu rõ thứ tự ưu tiên của các phép tính, như phép nhân/trừ trước, phép cộng/trừ sau. Nếu không nắm vững thứ tự ưu tiên này, kết quả khi học cách tính giá trị biểu thức lớp 9 có thể sai. Cũng như nếu không hiểu và áp dụng đúng các quy tắc toán học, như quy tắc gấp đôi, quy tắc phân phối, quy tắc kết hợp và quy tắc giao hoán thì có thể tính toán sai kết quả giá trị biểu thức lớp 9.

Khi không nắm vững lý thuyết sẽ dẫn đến hiểu sai hoặc nhầm lẫn trong quá trình học cách tính giá trị biểu thức lớp 9. Điều này có thể dẫn đến sai sót và kết quả không chính xác. Nắm vững lý thuyết giúp học sinh mở rộng kiến thức toán học và ứng dụng nó vào các bài toán phức tạp hơn. Khi đã hiểu rõ lý thuyết, học sinh hoàn toàn có khả năng áp dụng nó vào các vấn đề thực tế và giải quyết bài toán cách tính giá trị biểu thức lớp 9 một cách hiệu quả.
Các ký hiệu thường gặp và kiến thức cần nhớ trong dạng toán tính giá trị của biểu thức
Trong toán học, khi tính toán giá trị của biểu thức, có một số ký hiệu và kiến thức quan trọng cần nhớ, chẳng hạn như:
Căn bậc 2
Căn bậc 2 (hay còn gọi là căn bậc hai) của một số học là phép tính để tìm ra số gốc mà khi bình phương nó sẽ cho kết quả như mong muốn. Đối với một số dương xác định, căn bậc 2 được ký hiệu là √x.
Ở lớp 7 ta đã học:
- Nếu a lớn hơn hoặc bằng 0 [a≥0], căn bậc hai của a là x [√a = x] sao cho x bình phương bằng a [x2= a]
- Với a lớn hơn hoặc bằng 0 [a≥0] thì a có 2 căn bậc hai là căn bậc hai của a [√a] và âm căn a [-√a].
Lớp 9: Trường hợp a lớn hơn hoặc bằng 0 [a≥0] thì căn bậc hai của a là căn bậc hai số học a.
- x bằng căn bậc hai của a khi và chỉ khi x bình phương bằng a và x là số không âm [x = √a ⇔ ]
- Ví dụ: 9 có 2 căn bậc hai là 3 và -3; √ 9 bằng 3; -√9 = -3
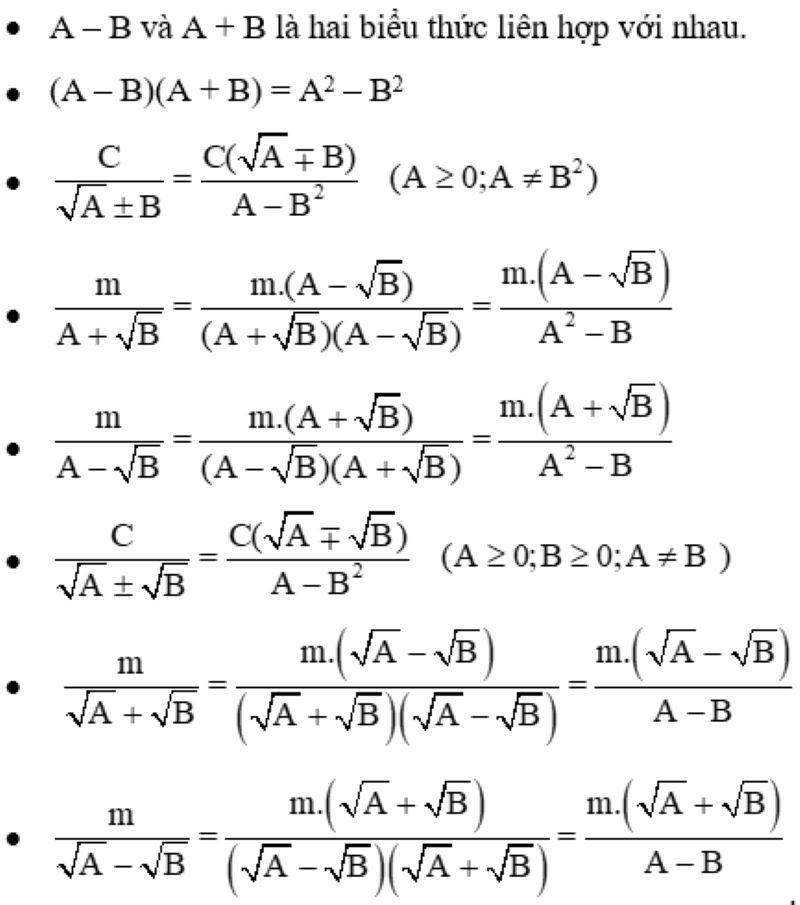
Trị tuyệt đối
Hằng đẳng thức căn bậc hai của A bình phương bằng trị tuyệt đối của A [√A2= |A|].
Ta có giá trị của A bằng chính nó nếu A lớn hơn hoặc bằng 0 và nếu giá trị A âm thì trị tuyệt đối của A bằng -A
- Ví dụ 1: √32 = 3; √(-3)2 = |-3| = -(-3) = 3
- Ví dụ 2: √x2y = |x|√y khi y≥0
- Ví dụ 3: 3√6 = √9.6 = √54; -3√6 = -√(-3)2.6 = -√54
Trị tuyệt đối của một số là giá trị dương của số đó, bỏ qua dấu. Để tính trị tuyệt đối của một số, bạn thực hiện các bước sau:
- Nếu số đó là dương, trị tuyệt đối của nó chính là chính nó.
- Nếu số đó là âm, trị tuyệt đối của nó được tính bằng cách đổi dấu của số đó.
- Ví dụ, |5| = 5 và |-8| = 8.
Phân số
Phân số là một biểu thức toán học gồm hai số được viết dưới dạng a/b, trong đó a được gọi là tử số và b được gọi là mẫu số. Tử số thể hiện phần đếm hoặc số lượng của đối tượng, trong khi mẫu số thể hiện phần chia hoặc số lượng phần bằng nhau mà đối tượng được chia thành. Lưu ý khi rút gọn phân số có ẩn số cần đặt điều kiện mẫu số khác 0.
Bình phương của một số
Bình phương của một số là kết quả của việc nhân số đó với chính nó. Ký hiệu bình phương của số a là a².
Công thức để tính bình phương của một số là a² = a.a
Ví dụ:
- Bình phương của số 4 là 4² = 4.4 = 16.
- Bình phương của số -3 là (-3)² = (-3).(-3) = 9.

Hướng dẫn cách tính giá trị biểu thức lớp 9 qua những dạng toán cụ thể
Dưới đây là các dạng toán cụ thể, kèm theo là các bước và ví dụ minh họa để học sinh có thể áp dụng kiến thức này vào thực tế.
Dạng 1: Biểu thức cần được rút gọn có chứa căn
Cách rút gọn biểu thức:
- Bước 1: Xác định điều kiện xác định cho biểu thức.
- Bước 2: Tìm mẫu thức chung, làm cho các mẫu thức có cùng mẫu số, rút gọn tử số, phân tích tử số thành các nhân tử.
- Bước 3: Chia cả tử số và mẫu số cho nhân tử chung của tử số và mẫu số.
- Bước 4: Tiếp tục rút gọn biểu thức cho đến khi không thể rút gọn được nữa.
Dạng 2: Cho biết trước x = x0, tính giá trị của biểu thức
Phương pháp:
- Bước 1: Rút gọn biểu thức A.
- Bước 2: Tại biểu thức đã rút gọn, thay giá trị x = x0 vào và tính kết quả.
- Dạng 3:Tìm biến x khi biểu thức A có giá trị bằng k (với k là hằng số)
Bài tập thực chiến
Ví dụ 1: Rút gọn biểu thức sau đây:
a) √(14+6√5) - √(14-6√5) = ???
b) √(√5+1)√(6-2√5) = ???
c) 15/(√6-1) +8/(√6+2) + 6/(3-√6) - 9√6 = ???
Hướng dẫn giải bài:
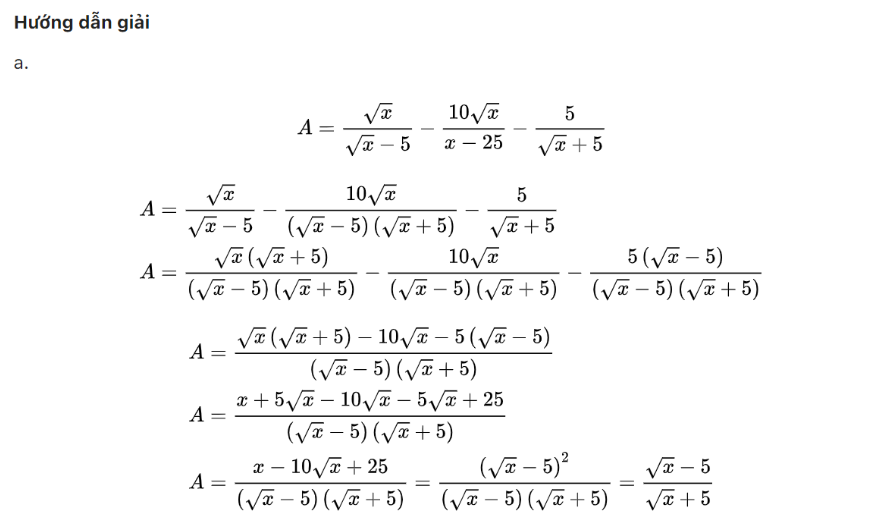
Ví dụ 2: Cho biểu thức sau đây:
Qua bài tổng hợp kiến thức lý thuyết cũng như bài tập vận dụng chi tiết, hy vọng có thể hỗ trợ học sinh ôn tập và làm bài thật tốt, dễ dàng giải quyết cách tính giá trị biểu thức lớp 9!