Cho hình chóp S.ABC có SA ^ (ABC). AB = a; \(AC = a\sqrt 2 ;\;\widehat {BAC} = 45^\circ \). Gọi B1, C1 lần lượt là hình chiều vuông góc của A lên SB, SC. Tính thể tích mặt cầu ngoại tiếp hình chóp A.BCC1B1.
Trả lời
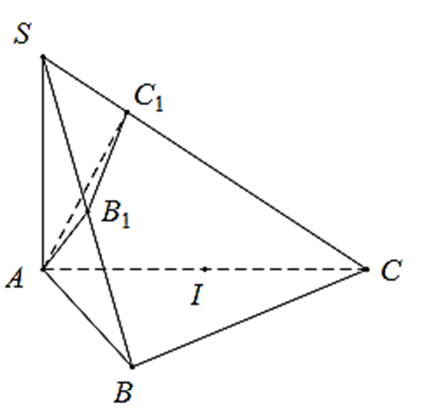
Tam giác ABC có AB = a; \(AC = a\sqrt 2 ;\;\widehat {BAC} = 45^\circ \) nên theo định lý cosin ta có:
BC2 = AB2 + AC2 − 2AB.AC.cos 45° = a2
Þ BC = a
Suy ra ∆ABC vuông cân tại B
Gọi I là trung điểm AC, ta có IA = IC = IB
Vì AC1 ^ SC nên IA = IC = IC1
Vì BC ^ SA, BC ^ AB
Þ BC ^ (SAB) Þ BC ^ AB1
Mà AB1 ^ SB Þ AB1 ^ (SBC)
Þ AB1 ^ B1C
Þ IA = IC = IB1
Vậy I là tâm mặt cầu ngoại tiếp chóp A.BCC1B1.
Bán kính của khối cầu đó là: \(R = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\).
Thể tích khối cầu đó là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {\frac{{a\sqrt 2 }}{2}} \right)^3} = \frac{{\pi {a^3}\sqrt 2 }}{3}\).
