Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \[2\sqrt 2 \], cạnh bên SA vuông góc với mặt đáy. Mặt phẳng (α) qua A và vuông góc với SC cắt các cạn SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tứ diện CMNP.
Trả lời
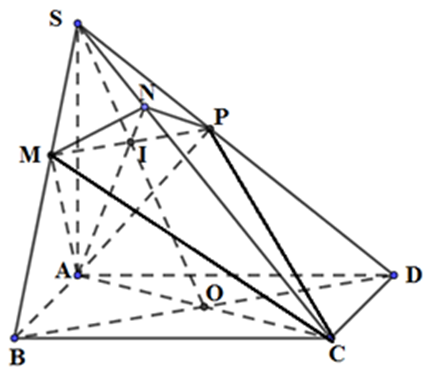
Gọi O là tâm của hình vuông ABCD ⇒O là trung điểm của AC
Ta có: CD ^ AD; CD ^ SA
Þ CD ^ (SAD)
Þ CD ^ AP
Lại có: SC ^ AP (do SC ⊥ (α)); CD ⊥ AP
⇒ AP ⊥ (SCD) ⇒ AP ⊥ CP ⇒ ΔAPC vuông tại P
⇒ OA = OC = OP
Tương tự, ta có: ΔAMC vuông tại M
⇒ OA = OC = OM
Lại có: SC ⊥ AN (do SC ⊥ (α))
⇒ΔANC vuông tại N ⇒OA = OC = ON
⇒ OA = OC = OP = OM = ON
Þ O là tâm mặt cầu ngoại tiếp tứ diện CMNP
Bán kính khối cầu là:
\[R = OA = \frac{{AB}}{{\sqrt 2 }} = 2\]
Thể tích khối cầu ngoại tiếp tứ diện CMNP là:
\[V = \frac{{4\pi }}{3} \cdot {2^3} = \frac{{32\pi }}{3}\]
Vậy thể tích khối cầu ngoại tiếp tứ diện CMNP là \[\frac{{32\pi }}{3}\].
