Trong mặt phẳng toạ độ Oxy cho ba điểm A(2; –1), B(1; 4) và C(7; 0). Tìm toạ độ của điểm D sao cho tứ giác ABDC là một hình vuông.
Trả lời
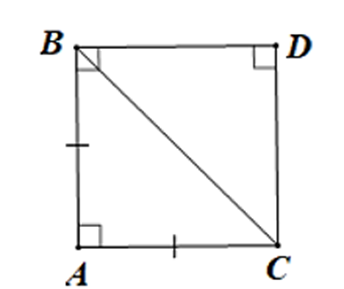
Vì ABC là tam giác vuông cân
Nên để ABDC là hình vuông thì tứ giác ABDC là hình bình hành
⇔ \(\overrightarrow {CA} = \overrightarrow {DB} \)
Gọi D(xD; yD) và có A(2; –1), B(1; 4), C(7; 0).
⇒ \(\overrightarrow {CA} = \left( { - 5; - 1} \right);\overrightarrow {DB} = \left( {1 - {x_D};4 - {y_D}} \right)\)
Do đó \(\overrightarrow {CA} = \overrightarrow {DB} \)
⇔ \(\left\{ \begin{array}{l} - 5 = 1 - {x_D}\\ - 1 = 4 - {y_D}\end{array} \right.\)
Vậy tọa độ điểm D cần tìm là D(6; 5).
